バイナリーサーチ(二分探索とも呼ばれる)はソート済みの配列において、検索する間隔を半分に分割しながらデータを探し出すアルゴリズムです。

ソート済みの配列を分割するということはバイナリーサーチツリーを生成することになります。

検索範囲の分割はデータの大小関係をもとに行われます。

アルゴリズム分析

1. 配列をソートする(ここでは昇順でソートされたとする)
2. 配列の中央にある要素を調べる
3. 探索
   • 中央の要素が目的の値ではなく、目的のデータが中央の値より大きい場合、中央より後半の部分を調べる
   • 中央の要素が目的の値ではなく、目的のデータが中央の値より小さい場合、中央より前半の部分を調べる
4. 2.に戻る

図解

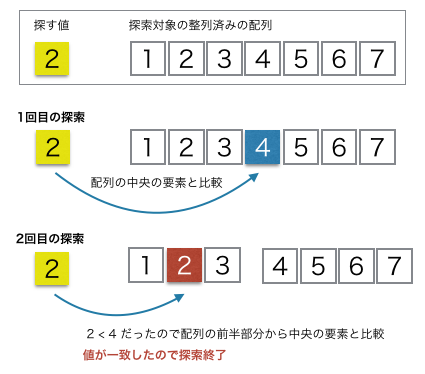
注意

バイナリーサーチは値の比較によって検索範囲を絞りこむので、探索対象の配列がソートされていなければなりません。

サンプルコード

配列から目的の値を検索するバイナリーサーチのサンプルコードです。

C言語

#include <stdio.h>

#define ARRAY_SIZE 7 /* size of array */

int main(void)
{
    int a[ARRAY_SIZE] = {1,2,3,4,5,6,7}; /* sorted array */
    int left = 0; /* start key of index */
    int right = ARRAY_SIZE; /* end key of index */
    int mid; /* middle key of index */
    int value; /* search value */

    puts("Find value?");
    scanf("%d", &value);

    while(left <= right) {
        mid = (left + right) / 2; /* calc of middle key */
        if (a[mid] == value) {
            puts("Found!\n");
            return 0;
        } else if (a[mid] < value) {
            left = mid + 1; /* adjustment of left(start) key */
        } else {
            right = mid - 1; /* adjustment of right(end) key */
        }
    }
    puts("Not Found.\n");
    return 0;
}

Python

def binary_search(l, value):
    low = 0
    high = len(l) - 1
    while low <= high:
        mid = (low + high) // 2
        if l[mid] == value:
            print('Found')
            return True
        elif l[mid] < value:
            low = mid + 1
        else:
            high = mid - 1
    print('Not Found')
    return False

#
# main
#
if __name__ == '__main__':
    import sys
    l = xrange(20)
    for num in l:
        assert binary_search(l, num)
    assert binary_search(l, -50) == False
    assert binary_search(l, -50) == False
    assert binary_search(l, 20) == False
    assert binary_search(l, 19) == True
    assert binary_search(l, 0) == True
    assert binary_search([1,2,4,12,67,90], 3) == False

• リニアサーチ
• バブルソート

---