ヒープは半順序集合をツリーで表現したデータ構造です。親ノードは、子ノードよりも小さい(あるいは大きい)か等しいという条件を満たすツリー構造になります。子の関係に制約はありません。あくまで親子間での制約です。

単にヒープと呼ぶ場合、バイナリツリーとして構成されるバイナリヒープを指すことが多いです。

Infoコンピュータ サイエンスでヒープと言う場合「ヒープ領域」を指すこともありますので間違わないようにしましょう。

特徴 - ヒープ プロパティ

親子の関係によってヒープの性質 - ヒープ プロパティ [heap property] は2種類に分かれます。

最大ヒープ [max-heap property]

親ノードは子ノードより大きいか等しい。

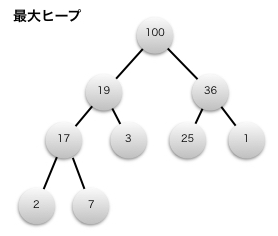
最小ヒープ [min-heap property]

親ノードは子ノードより小さいか等しい。

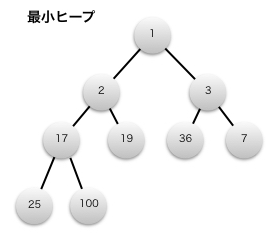
プロパティによりルートノードは常に最大あるいは最小要素となります。ヒープはこういった特徴から、抽象データ型であるプライオリティ キュー [priority queue] (優先順位付き待ち行列とも呼ばれる)のデータ構造として利用されます。また、ヒープを用いた整列アルゴリズムに、ヒープソートというものがあります。

実装

ヒープ(バイナリヒープ)は配列を使って実現されます。ツリーの高さは高さ n の要素が使用されるまで、高さ n+1 の要素を作成しません。

インデックスを 1 から開始するとノード n の親ノードは n/2、子ノードは 2n と 2n+1 でアクセスできます。

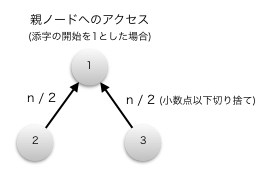
親ノードのインデックスを計算する除算 n/2 は小数点以下を切り捨てます。

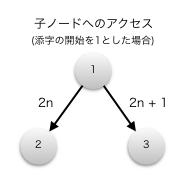
インデックスを 0 から開始すると親ノードは (n - 1) / 2、子ノードは 2n + 1 と 2n + 2 になります。

サンプルコード

C言語

配列で最大ヒープ [max-heap] を作成する関数です。

/* max-heap property */
void insert(int val, int heap[], int counter)
{
    int i = counter + 1;
    while( (i != 1) && (heap[i/2] < val) ) {
        heap[i] = heap[i/2];
        i = i/2;
    }
    heap[i] = val;
}

Python

配列で最大ヒープ [max-heap] を作成します。

def insert(val, heap, counter):
    i = counter
    while ((i != 1) and (heap[i/2] < val)):
        heap[i] = heap[i/2]
        i = i / 2
    heap[i] = val

• バランスドツリー(平衡木)
• アルゴリズム

---