本ページには広告・プロモーションが含まれています。
自己相関
自己相関の説明
自己相関とは 時系列データ について、自分自身の過去のデータとどのくらい関連がありそうかを調べる手法。
相関 では 異なる変数の関係性を分析するが、この概念を時系列分析に応用して、 自身の過去のデータとの関連性を調べることで「似ている時期」や「でたらめさ」を分析できる。
具体的にはデータの時点をひとつ前の時点やふたつ前にずらした新しい変数を作って相関係数を算出する。
時点のズレをラグ(遅れ)と言う。また、ラグを横軸に、相関係数を縦軸にした棒グラフをコレログラムと呼ぶ。
ナンバーズの予想に使うには
基本的には時系列解析なので何回前の抽せん数字に出現傾向が似ているかや不規則な変動を明らかにする。
相関が見られる時点のデータを使って 回帰分析 を行うことで次回の抽せん数字を予測することも可能。
分析の注意点としては
自己相関がある時系列データで回帰分析を行うと、決定係数が非常に高く出る場合がある。こういった場合の回帰モデルは有用とは言えないので注意しなければならない。 この場合、対策として差分(当日と前日のデータの差)を計算することが多い。
「 見せかけの回帰 」というのが起きるので階差(変数の差分)を取って分析する。
100の位の抽せん数字の自己相関分析
例として第1回から第100回の100の位の抽せん数字について自己相関を分析してみる。
毎度のことながら本来は質的データである抽せん数字を量的データとして扱うことに注意。
python プログラムは 前準備 で用意したデータフレームを使っている。
まずは階差を取らない生の時系列データの相関係数を確認しよう。
# t0 が元のデータ, t1 は t0 からひとつ前の回号の抽せん数字、
# t2 は t0 からふたつ前の回号の抽せん数字
p100 = pd.concat(dict(t0=df.loc[1:100, 'place100'], \
t1=df.loc[1:100, 'place100'].shift(1), \
t2=df.loc[1:100, 'place100'].shift(2)), \
axis=1)
# 相関係数
p100.corr()
| t0 | t1 | t2 | |
|---|---|---|---|
| t0 | 1.000000 | 0.061209 | 0.070276 |
| t1 | 0.061209 | 1.000000 | 0.060972 |
| t2 | 0.070276 | 0.060972 | 1.000000 |
t1 と t2 の相関は無視するとして、1時点前である t0 と t1 の相関係数は 0.06 、2時点前である t0 と t2 の相関係数は 0.07 ということでほとんど相関はないと言えそう。
次に階差を取ったデータの相関係数を確認する。
p100diff = pd.DataFrame(dict(t0=p100.t0 - p100.t0.shift(1)))
p100diff['t1'] = p100diff.t0.shift(1)
p100diff['t2'] = p100diff.t0.shift(2)
p100diff.corr()
| t0 | t1 | t2 | |
|---|---|---|---|
| t0 | 1.000000 | -0.498674 | 0.051945 |
| t1 | -0.498674 | 1.000000 | -0.500048 |
| t2 | 0.051945 | -0.500048 | 1.000000 |
こちらも t1 と t2の相関は無視するとして、1時点前である t0 と t1 の相関係数は -0.5 であり負の相関があると言える結果を得られた。2時点前である t0 と t2 の相関係数は 0.05 ということでほとんど相関はないと言える。
Python Tips
ここまで pandas.DataFrame を使って相関係数を調べた、自己相関係数を一発で調べるには pandas.Series の autocorr を使う。
# 階差なし
# ラグ 1、ラグ 2で計算
p100.t0.autocorr(lag=1), p100.t0.autocorr(lag=2)
# 結果 (0.061209210845076856, 0.07027621623378515)
# 階差あり
# ラグ 1、ラグ 2で計算
p100diff.t0.autocorr(lag=1), p100diff.t0.autocorr(lag=2)
# 結果 (-0.49867362102628304, 0.05194506923750513)
パラメータ lag で時点のズレを指定できるので lag をインクリメントして計算すると自動で多くのデータを手に入れることができる。
相関係数をリストで取得する関数の例:
def autocorr(series):
lags = range(len(series)//2) # 個体数の半分
corrs = [series.autocorr(lag) for lag in lags]
return lags, corrs
コレログラム
ラグを横軸に、相関係数を縦軸にした棒グラフをコレログラム(自己相関プロット)と呼ぶ。
一度に複数時点の相関係数をプロットして、相関が見られる時点を分析しよう。
まずは前処理なしの時系列データを棒グラフで描いてみる。
lags,corrs = autocorr(p100.t0) # 上記で定義した関数を使う
plt.figure(figsize=(8,6))
plt.xlabel('ラグ')
plt.ylabel('自己相関係数')
plt.title('自己相関係数 : 第1回から第100回の100の位の抽せん数字', fontsize=12)
plt.bar(x=lags, height=corrs)

ラグが無い 0 時点は当然相関係数は 1.0 なので無視するとして、 上のグラフから読み取れること:
- ラグ41には弱い正の相関が見られる
- ラグ14には弱い負の相関が見られる
- 周期的な変動はなさそう
- 見せかけの回帰があるかもしれない
見せかけの回帰を回避した、階差のコレログラムを描いてみる。
lags,corrs = autocorr(p100diff.t0) # 上記で定義した関数を使う
plt.figure(figsize=(8,6))
plt.xlabel('ラグ')
plt.ylabel('自己相関係数')
plt.title('階差による自己相関係数 : 第1回から第100回の100の位の抽せん数字', fontsize=12)
plt.bar(x=lags, height=corrs)
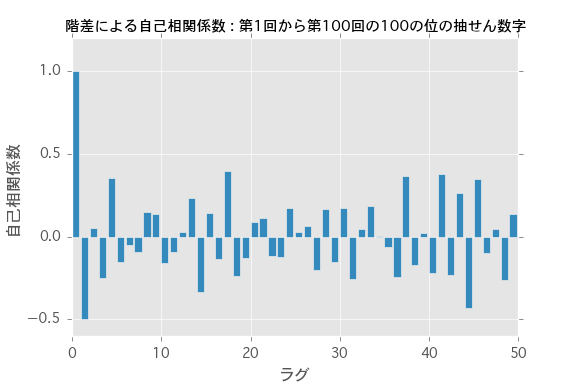
1.0 の時点はラグが無い 0 なので無視するとして、 上のグラフから読み取れること:
- ラグ1に負の相関が見られる
- ラグ17には正の相関が見られる
- しかしながら周期的な変動はなさそう
参考文献
最終更新日: 2020年01月17日(金)
目次
プロローグ
- はじめに
- ナンバーズの予想・攻略方法
- 前準備 (ナンバーズ3のデータの準備と統計解析の環境について)
統計解析
データマイニング
- マルコフ連鎖 (ひとつ前の過去が未来を決定する)
- アソシエーション分析 (よくある組み合わせを発見する)
- 決定木 (要因を分析して未来を予測する)
- サポートベクターマシン (パターン認識)



