本ページには広告・プロモーションが含まれています。
相関係数と散布図
相関係数とは
相関係数とは 2つの変数の間にどのような関係があるかを数値的に示したもの 。
「一方の値が増加すると、他方の値が増加または減少するのか?」という2つの変量の関係を数値として表すのが相関係数。
相関係数は -1 から 1 の範囲におさまる が、数値が意味すること(相関の解釈)は慣例的に下表の通り。
| 相関係数 | 相関の強さ |
|---|---|
| 0.0~±0.2 | (ほとんど)相関がない |
| ±0.2~±0.4 | 弱い相関がある |
| ±0.4~±0.7 | 相関がある |
| ±0.7~±0.9 | 強い相関がある |
| ±0.9~±1.0 | (ほぼ)完全な相関がある |
相関係数がプラスの時は一方が大きくなれば他方も大きくなるという右肩上がりの関係になり、 マイナスの相関係数は一方が小さくなれば他方も小さくなるという右肩下がりの関係になる。
相関係数の例
相関(2つの変量の関係)の分析は、主として 時間とともに変量が増加または減少するデータの分析 に有効である。
ナンバーズの場合だと抽せん数字というのは足したり引いたりするものではない(※)のだが、 「一方が大きくなれば他方も大きくなる」というのをわかりやすく示すために、 位ごとの抽せん数字を足し合わせた 累積度数 を作成して分析してみる。
(※)抽せん数字というのはあくまでラベルである。0から9の数字を「ABCDEFGHI」の英字だと考えると理解できると思います。
| 100の位 | 10の位 | 1の位 | |
|---|---|---|---|
| 回号 | |||
| 1 | 1 | 9 | 1 |
| 2 | 10 | 17 | 9 |
| 3 | 11 | 26 | 13 |
| 4 | 12 | 26 | 18 |
| 5 | 17 | 35 | 20 |
| 6 | 24 | 44 | 22 |
| 7 | 31 | 44 | 30 |
| 8 | 33 | 47 | 34 |
| 9 | 35 | 51 | 37 |
| 10 | 38 | 55 | 37 |
上の表を作成して相関係数を計算してみます。
python のプログラムは 前準備 で用意したデータフレームを使っています。
# 第1回から第10回の抽せん数字の位ごとの累積度数分布表
df_cumsum = df.loc[1:10,['place100', 'place10', 'place1']].cumsum()
df_cumsum.columns = ['100の位', '10の位', '1の位'] # カラム名変更
# 相関係数を計算
df_cumsum.corr()
# corr() の 結果
# 100の位 10の位 1の位
# 100の位 1.000000 0.974706 0.981734
# 10の位 0.974706 1.000000 0.969546
# 1の位 0.981734 0.969546 1.000000
「1.000000」となっているところは同じ変数の相関である。
注目する相関係数は以下の3つの箇所だ。
- 100の位と10の位: 0.974706
- 100の位と1の位: 0.981734
- 10の位と1の位: 0.969546
いずれも相関分析は 0.9 以上となっており、『完全な相関がある』と解釈する。
※ここでの例は『「一方が大きくなれば他方も大きくなる」というのをわかりやすく示すために』作られた度数分布表を用いていることに注意。 相関係数が高くなるのは当たり前の結果です。
散布図
散布図とは2つの変量を図にしたものである。
『第1回から第10回 抽せん数字の位ごとの累積度数分布表』から100の位と10の位を散布図として描いたのが下の図である。

# 散布図を描画
df_cumsum.plot(kind='scatter', x='100の位', y='10の位', title='100の位と10の位の散布図', figsize=(7.4, 5.8))
散布図は相関を視覚的に把握できるメリットがあり、 『相関係数と相関の強さ』のように 散布図の形から相関の強さを読み取る ことができる。 その形は5種類ある。
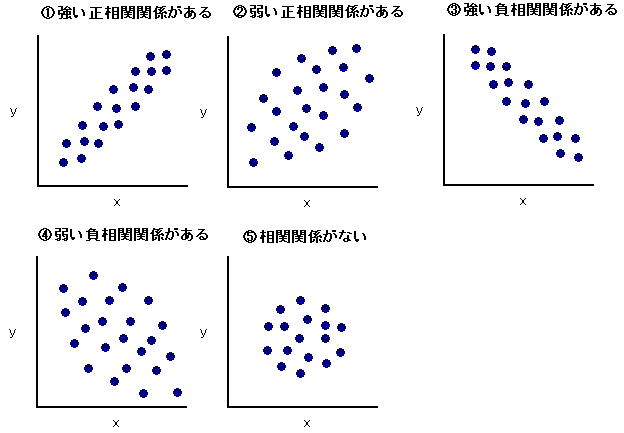
出典: https://web.archive.org/web/20160328085526/http://www.sqc-works.com/qc7-04.html
ナンバーズの予想に使うには
相関の分析は2つの変数(項目)の関係を示す値であることから、 相関係数の高い2つの項目を発見することがナンバーズの予想につながる。
一般的に相関分析でよくある例:
- 気温とアイスクリームの売上: 気温が高い時にアイスクリームはよく売れるのか?
- 身長と体重: 背の高い人は体重も多いのか?
- 人口と出生児数: 人間が多いほど生まれてくる赤ちゃんも多いのか?
相関分析は増加したり減少したりする数の分析に有効 である。 ナンバーズの抽せん数字は、数字というよりも000から999の「ラベル」であるため増減する変量を自分で考えてデータを出すことが必要だ。
参考文献
最終更新日: 2020年01月10日(金)
目次
プロローグ
- はじめに
- ナンバーズの予想・攻略方法
- 前準備 (ナンバーズ3のデータの準備と統計解析の環境について)
統計解析
データマイニング
- マルコフ連鎖 (ひとつ前の過去が未来を決定する)
- アソシエーション分析 (よくある組み合わせを発見する)
- 決定木 (要因を分析して未来を予測する)
- サポートベクターマシン (パターン認識)